Celestial coordinate system
 Orientation of the galactic, ecliptic and equatorial coordinate systems, projected on the celestial sphere, showing the galactic equator (black), north galactic pole (NGP), the ecliptic (orange), north ecliptic pole (NEP), the celestial equator (blue) abd north celestial pole (NCP). Sun and earth not shown to scale but to indicate sun's orbital direction around the galactic center and earth's orbital direction around the sun. |
In astronomy, a celestial coordinate system is a coordinate system for mapping positions on the celestial sphere. There are different celestial coordinate systems each using a system of spherical coordinates projected on the celestial sphere, in analogy to the geographic coordinate system used on the surface of the Earth. The coordinate systems differ only in their choice of the fundamental plane, which divides the sky into two equal hemispheres along a great circle. For example, the fundamental plane of the geographic system is the Earth's equator. Each coordinate system is named for its choice of fundamental plane.
Contents |
Coordinate systems
| Coordinate system | Fundamental plane | Poles | Coordinates |
|---|---|---|---|
| Horizontal (also called Alt/Az or Az/El) |
horizon | zenith/nadir | elevation (also called altitude) - azimuth - meridian |
| Equatorial | celestial equator | celestial poles | declination - right ascension or hour angle |
| Ecliptic | ecliptic | ecliptic poles | ecliptic latitude - ecliptic longitude |
| Galactic | galactic plane | galactic poles | |
| Supergalactic | supergalactic plane |
Horizontal system
The horizontal, or altazimutal, system is based on the position of the observer on earth, which revolves around its own axis once per sidereal day (23.hours, 56 minutes and 4.091 seconds) in relation to the "fixed" star background. The positioning of a celestial object by the horizontal system is therefore ephemeral, and used mainly for computation of times of rising or setting, f.ex. sunrise and sunset. Of old it was also used for navigation, such as determining a planets altazimutal position, with accurate timing, and therefrom determining the latitude and longitude of the traveling ship. Many telescopes also use altazimutal mounts, but then computing the horizontal position from time, geographic position and the objects' position is typically performed by computer.
Equatorial system
The equatorial coordinate system is centered at Earth's center and fixes the sky around us, so that it appears fixed while earth, and we on its surface, revolves around its own axis. The equatorial describes the sky, as seen from the solar system, and modern star maps are almost exclusively perusing equatorial coordinates. Ancient Eastern astronomers used this for their star charts.
The equatorial system is the normal coordinate system for most professional and many amateur astronomers having an equatorial mount that follows the movement of the sky during the night. Celestial objects are found by adjusting the telescope's or other instrument's scales so that they match the equatorial coordinates of the selected object to observe.
Popular choices of pole and equator are the older B1950 and the modern J2000 systems, but a pole and equator "of date" can also be used, meaning one appropriate to the date under consideration, such as that at which a measurement of the position of a planet or spacecraft is made. There are also subdivisions into "mean of date" coordinates, which average out or ignore nutation, and "true of date," which include nutation.
Ecliptical system
The ecliptical system was one of the old coordinate systems used for star maps before astronomy and astrology divorced, particularly in the West.
The ecliptical system describes the planets' orbital movement around the sun, and centers on the barycenter of the solar system, which is in the sun. The fundamental plane is the plane wherein earth orbits, called the ecliptical plane. It is in heavy use for planetary science, such as computing planet positions and other important planet metrics, inclination, ascending and descending nodes, position of perihelion and so on.
Galactic system
The galactic system has our solar system as the center, a position nearly pointing towards the center of the Milky way as the zero direction, and otherwise has a fundamental plane that approximately coincides with the disk of the Milky Way, but which is fixed by standard. The galactic system is of course used for interstellar positioning of objects in relation to our galaxy.
Supergalactic system
Altitude
Altitude, also referred to as elevation angle, refers to the vertical angle measured from the astronomical horizon (0°) towards the zenith (+90°). It can also take negative values for objects below the horizon, down to the nadir (-90°). Although some will use the term height instead of elevation, this is not recommended as height is usually understood to be a linear distance unit, to be expressed in meters (or any other length unit), and not an angular distance.
The term zenith distance is more often used in astronomy and is the complement of the elevation. That is: 0° in the zenith, 90° on the horizon, up to 180° at the nadir.
Converting coordinates
Equatorial to horizontal coordinates
Let δ be the declination and  the hour angle.
the hour angle.
Let φ be the observer's latitude.
Let a be the altitude and A the azimuth.
Let θ be the zenith (or zenith distance, i.e. the 90° complement of Alt).
Then the equations of the transformation are:
Use the inverse trigonometric functions to get the values of the coordinates.
NOTE: Inverse cosine is dual valued, i.e. 160° and 200° both have the same cosine. The above needs to be corrected. If H < 180 (or Pi radians) then Az = 360 - Az as derived from the above equation.
See also
- Axial tilt
- Azimuth
- Inclination
- Kozai effect
- Orbital inclination change
External links
- This article was originally based on Jason Harris' Astroinfo which comes along with KStars, a KDE Desktop Planetarium for Linux/KDE.
|
||||||||||||||||||||||||||||||||||||||||||||||



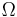



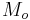
 True anomaly
True anomaly Semi-minor axis
Semi-minor axis
 Eccentric anomaly
Eccentric anomaly Mean longitude
Mean longitude True longitude
True longitude